
28 September 2007
Détermination du Rendement Quantique (QE) d'un capteur CMOS
Bonjour à tous,
Suite à de nombreuses questions qui me sont régulièrement posées concernant le rendement quantique des capteurs CMOS qui équipent les APN de chez Canon, je me suis enfin décidé à écrire une petite note concernant la détermination de cette importante caractéristique.
Tout d’abord, pourquoi cette donnée est-elle si importante aux yeux des astrophotographes ? Pour répondre à cette question, il faut se rappeler la notion de rapport signal/bruit (S/B) d’une image numérique. A titre d’exemple, la photo suivante illustre le problème : il s’agit d’une portion agrandie de la nébuleuse Veil en exagérant les seuils afin de mieux révéler le bruit du fond de ciel. Les poses sont de 20 minutes avec un APN Canon 300D défiltré (sans filtre infrarouge), ce qui garantit que le bruit électronique est marginal face au bruit photonique du fond de ciel. Une coupe du signal (en ADU) est superposé au cliché pour bien mettre en évidence le bruit du fond de ciel.
Le bruit lié à la variation aléatoire du signal empêche de discerner les détails dans les faibles voilures de la nébuleuse, et plus particulièrement sur les pourtours de celle-ci, à la transition avec le fond de ciel. Pour mieux faire apparaître ces détails, il faut augmenter au maximum le rapport S/B. Dans le cas qui nous occupe, le bruit de lecture du capteur est marginal par rapport au bruit photonique. Ce dernier résulte du fait que l’émission de photons n’est pas un phénomène parfaitement constant dans le temps, mais répond à une distribution statistique qui est bien décrite par la loi dite de « Poisson ». Un propriété importante de cette statistique est la suivante : si le nombre moyen de photons captés par chaque pixels du capteur est Np, des variations aléatoires de pixel à pixel apparaîtront avec un écart-type donné par la racine carrée de Np, sqrt(Np), même pour des pixels idéalement identiques. Autrement dit, le rapport S/B du signal photonique est donné par Np/sqrt(Np), soit encore sqrt(Np).
L’augmentation du rapport S/B passe donc par l’accroissement de signal. Et c’est ici qu’intervient le rendement quantique du capteur. Un capteur numérique consiste essentiellement en un convertisseur photoélectrique dans lequel le photon est converti en électron. Cette conversion n’est malheureusement pas pas parfaite et seulement un certain pourcentage de ces photons incidents seront convertis, ce qui définit le rendement quantique. Le rapport S/B de l’image étant liée au nombre d’électrons générés , il est donc impératif d’optimiser ce rendement quantique. Une conséquence importante de ces considérations est l’impact que le capteur a sur le dimensionnement d’un télescope : pour une même détectivité, un rendement quantique double permet de réduire la surface collectrice par deux, avec toutes les implications que cela présente sur le poids total de l’installation ainsi que son prix de revient (exponentiel avec la surface collectrice pour les grandes installations ! !)
A l’heure actuelle, les capteurs CCD conventionnels atteignent facilement des rendements honorables, même au niveau amateur (au delà des 80%), à condition d’être refroidi convenablement pour réduire l’effet du bruit thermique. Avec l’avènement récent des capteurs CMOS à très bas bruit de lecture et signal thermique (principalement chez Canon), beaucoup d’amateurs se sont tournés vers ce type de produits qui présentent des surfaces importantes à des prix défiant toute concurrence. Cependant, il leur est généralement reproché un rendement quantique beaucoup plus faible par rapport aux CCD conventionnelles, ceci étant dû entre autre à la technologie mise en oeuvre. C’est justement l’objet de cette note d’apporter un éclaircissement sur ce point en déterminant le rendement quantique du capteur CMOS d’un APN Canon 300D défiltré.
Quand il est fourni par le constructeur, le rendement quantique est obtenu à l’aide de sources de lumières calibrées dont le coût est prohibitif pour l’amateur que nous sommes. Il n’est cependant pas nécessaire d’acheter une source standard de lumière pour effectuer ce travail étant donné que le ciel nous fournit une panoplie de sources particulièrement bien documentées par le monde des professionnels, à savoir les étoiles. Parmi elles, l’étoile Véga (Alpha de la Lyre) a reçu une attention particulière, notamment pour la quantification précise du spectre de sa lumière (hors atmosphère):
L’idée est alors de réaliser une photographie de l’étoile Véga avec l’APN au foyer d’une lunette, dans ce cas-ci une TAKAHASHI FSQ106N ouverte à f5. La mesure du rendement quantique consiste donc à calculer le nombre de photons en provenance de Véga qui atteignent le capteur (sur base de la figure ci-dessus) et à le comparer au nombre d’électrons générés au sein des pixels. Cette mesure électronique s’effectuera à l’aide des outils de photométrie intégrés dans le logiciel IRIS développé par Christian BUIL.
Pour établir le nombre de photons entrant dans la lunette, la largeur de la fenêtre spectrale doit être déterminée avec suffisamment de précision. A cette fin, un filtre anti-pollution Baader-UHC a été monté à l’avant de l’APN. Un problème supplémentaire rencontré pour caractériser les capteurs couleurs est la présence des filtres disposés au-dessus de chaque pixel du capteur conformément à la matrice dite de « Bayer » et qui permettent de reconstituer l’image couleur par des techniques d’interpolation (voir BUIL). Un exemple de cette matrice est donné à la figure suivante :
Un moyen de s’affranchir de ce problème est de ne prendre que les pixels d’une des couleurs, par exemple les rouges et de les rassembler sur une même image. Ceci peut être facilement réalisé à l’aide d’une fonction particulière d’IRIS, à savoir la commande SPLIT_CFA V1 V2 V3 V4 . Attention dans la mesure du nombre d’électrons, il faudra tenir compte du fait que la mesure photométrique ne s’effectuera plus que sur 1 pixel sur quatre (le rouge) et le bilan électronique devra ainsi être multiplié par 4 pour restituer le nombre total d’électrons générés par les photons émis par Véga.
L’image V3.pic ainsi créée concerne les pixels rouges dont il faut maintenant établir la transmission spectrale. Sur base de document de chez Canon (voir Wang) , il apparaît que la courbe de transmission du filtre rouge de la matrice de Bayer (en médaillon sur la figure suivante) est de type filtre passe-haut à partir de 600nm qui englobe largement la réponse du filtre Baader-UHC .
C’est donc la fenêtre autour du pic Ha dans le rouge de ce filtre UHC qui définit la fenêtre spectrale, à savoir une largeur de 500A pour une longueur d’onde d’environ 6565A. Le calcul du nombre de photons entrant s’établit sur base de la réponse spectrale de Véga autour du pic Ha :
Débit photonique (en puissance) = 2.10-8 W/m2/µm = 2.10-16 J/s/cm2/A
Pour convertir ce résultat en nombre de photons, il est nécessaire de calculer l’énergie E d’un photon de longueur d’onde lamda=6565A
E = h.c / lamda
où h=6.62.10-34 est la constante de Planck et c=3.10+8 m/s est la vitesse de la lumière. L’énergie des photons étant d’environ 3 .10-19 J, le débit s’écrit :
Débit photonique = 666 photons/s/cm2/A
Pour une fenêtre de 500A et un temps de pose de 1s, le nombre de photons capturés par la surface collectrice de la lunette (=88 cm2) est finalement de 30.10+6 photons. Il faut cependant réduire ce résultat pour tenir compte de l’absorption atmosphérique et de la transmission optique de la lunette qui comporte 4 lentilles, soit encore 8 interfaces verre/air. Si la perte par interface est de l’ordre de 1 pourcent (revêtement multicouches de qualité), la perte pour l’optique est d’environ 8 pourcents, soit 92% de transmission. En ce qui concerne les pertes dans l’atmosphère, le graphe suivant permet d’évaluer la transmission à environ 75% à 6500A (Véga était proche du zénith et l’altitude du lieu d’observation proche de 0m). In fine, le nombre de photons collectés est donc de 21.10+6 photons.
En photométrie d’ouverture (menu Analyse dans IRIS), l’intensité photométrique intégrée sur l’ensemble de l’image de Véga défocalisée s’élève à 480000 ADU. A partir du gain mesuré sur le Canon 300D (sa mesure sera l’objet d’une prochaine note), soit 2.4 électrons/ADU, la quantité totale d’électrons générés par Véga est donc de 4 X (480000 X 2.4) = 4.6.10+6 électrons.
Le rendement quantique (QE – Quantum Efficiency) du capteur CMOS de l’APN Canon 300D défiltré est finalement :
QE = 4.600.000 / 21.000.000 = 22%
Pour ceux que cela intéresse, j’ai synthétisé ce calcul sur une feuille Excel qui reprend tous les éléments nécessaires à l’évaluation du rendement quantique (voir figure ci-dessous). N’importe quelle étoile peut être utilisée pour cette mesure, pour autant que sa magnitude visuelle m, sa température effective Te et son indice bolométrique BC (ou encore son indice B-V ) soient connus. Je peux l’envoyer sur demande postée à mon adresse email : schmitz_a@swing.be
Ce résultat est en accord avec d’autres résultats de la littérature (voir Clark), et se situe bien en-dessous des performances atteintes par les CCD classiques. Différentes explications plausibles sont à avancer, dont notamment le facteur de remplissage beaucoup moins élevé lié à la technologie APS (Active Pixel Sensor, dans laquelle des composants actifs limitent la zone de conversion photoéléctrique des pixels).
D’un point de vue pratique pour l’amateur, il faudra donc s’attendre à exposer quatre fois plus longtemps avec ce genre d’appareil pour atteindre un rapport S/B équivalent à une CCD SBIG ST10, mais aussi à un prix 10 fois moindre ! Mais comme l’astrophotographie est une école de patience, le passionné mettra le temps nécessaire pour obtenir, somme toute, de très bonnes images comme il en pleut déjà au travers des revues et des sites web.
Alain SCHMITZ
Suite à de nombreuses questions qui me sont régulièrement posées concernant le rendement quantique des capteurs CMOS qui équipent les APN de chez Canon, je me suis enfin décidé à écrire une petite note concernant la détermination de cette importante caractéristique.
Tout d’abord, pourquoi cette donnée est-elle si importante aux yeux des astrophotographes ? Pour répondre à cette question, il faut se rappeler la notion de rapport signal/bruit (S/B) d’une image numérique. A titre d’exemple, la photo suivante illustre le problème : il s’agit d’une portion agrandie de la nébuleuse Veil en exagérant les seuils afin de mieux révéler le bruit du fond de ciel. Les poses sont de 20 minutes avec un APN Canon 300D défiltré (sans filtre infrarouge), ce qui garantit que le bruit électronique est marginal face au bruit photonique du fond de ciel. Une coupe du signal (en ADU) est superposé au cliché pour bien mettre en évidence le bruit du fond de ciel.
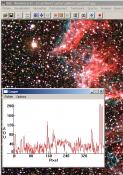
Le bruit lié à la variation aléatoire du signal empêche de discerner les détails dans les faibles voilures de la nébuleuse, et plus particulièrement sur les pourtours de celle-ci, à la transition avec le fond de ciel. Pour mieux faire apparaître ces détails, il faut augmenter au maximum le rapport S/B. Dans le cas qui nous occupe, le bruit de lecture du capteur est marginal par rapport au bruit photonique. Ce dernier résulte du fait que l’émission de photons n’est pas un phénomène parfaitement constant dans le temps, mais répond à une distribution statistique qui est bien décrite par la loi dite de « Poisson ». Un propriété importante de cette statistique est la suivante : si le nombre moyen de photons captés par chaque pixels du capteur est Np, des variations aléatoires de pixel à pixel apparaîtront avec un écart-type donné par la racine carrée de Np, sqrt(Np), même pour des pixels idéalement identiques. Autrement dit, le rapport S/B du signal photonique est donné par Np/sqrt(Np), soit encore sqrt(Np).
L’augmentation du rapport S/B passe donc par l’accroissement de signal. Et c’est ici qu’intervient le rendement quantique du capteur. Un capteur numérique consiste essentiellement en un convertisseur photoélectrique dans lequel le photon est converti en électron. Cette conversion n’est malheureusement pas pas parfaite et seulement un certain pourcentage de ces photons incidents seront convertis, ce qui définit le rendement quantique. Le rapport S/B de l’image étant liée au nombre d’électrons générés , il est donc impératif d’optimiser ce rendement quantique. Une conséquence importante de ces considérations est l’impact que le capteur a sur le dimensionnement d’un télescope : pour une même détectivité, un rendement quantique double permet de réduire la surface collectrice par deux, avec toutes les implications que cela présente sur le poids total de l’installation ainsi que son prix de revient (exponentiel avec la surface collectrice pour les grandes installations ! !)
A l’heure actuelle, les capteurs CCD conventionnels atteignent facilement des rendements honorables, même au niveau amateur (au delà des 80%), à condition d’être refroidi convenablement pour réduire l’effet du bruit thermique. Avec l’avènement récent des capteurs CMOS à très bas bruit de lecture et signal thermique (principalement chez Canon), beaucoup d’amateurs se sont tournés vers ce type de produits qui présentent des surfaces importantes à des prix défiant toute concurrence. Cependant, il leur est généralement reproché un rendement quantique beaucoup plus faible par rapport aux CCD conventionnelles, ceci étant dû entre autre à la technologie mise en oeuvre. C’est justement l’objet de cette note d’apporter un éclaircissement sur ce point en déterminant le rendement quantique du capteur CMOS d’un APN Canon 300D défiltré.
Quand il est fourni par le constructeur, le rendement quantique est obtenu à l’aide de sources de lumières calibrées dont le coût est prohibitif pour l’amateur que nous sommes. Il n’est cependant pas nécessaire d’acheter une source standard de lumière pour effectuer ce travail étant donné que le ciel nous fournit une panoplie de sources particulièrement bien documentées par le monde des professionnels, à savoir les étoiles. Parmi elles, l’étoile Véga (Alpha de la Lyre) a reçu une attention particulière, notamment pour la quantification précise du spectre de sa lumière (hors atmosphère):
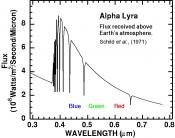
L’idée est alors de réaliser une photographie de l’étoile Véga avec l’APN au foyer d’une lunette, dans ce cas-ci une TAKAHASHI FSQ106N ouverte à f5. La mesure du rendement quantique consiste donc à calculer le nombre de photons en provenance de Véga qui atteignent le capteur (sur base de la figure ci-dessus) et à le comparer au nombre d’électrons générés au sein des pixels. Cette mesure électronique s’effectuera à l’aide des outils de photométrie intégrés dans le logiciel IRIS développé par Christian BUIL.
Pour établir le nombre de photons entrant dans la lunette, la largeur de la fenêtre spectrale doit être déterminée avec suffisamment de précision. A cette fin, un filtre anti-pollution Baader-UHC a été monté à l’avant de l’APN. Un problème supplémentaire rencontré pour caractériser les capteurs couleurs est la présence des filtres disposés au-dessus de chaque pixel du capteur conformément à la matrice dite de « Bayer » et qui permettent de reconstituer l’image couleur par des techniques d’interpolation (voir BUIL). Un exemple de cette matrice est donné à la figure suivante :

Un moyen de s’affranchir de ce problème est de ne prendre que les pixels d’une des couleurs, par exemple les rouges et de les rassembler sur une même image. Ceci peut être facilement réalisé à l’aide d’une fonction particulière d’IRIS, à savoir la commande SPLIT_CFA V1 V2 V3 V4 . Attention dans la mesure du nombre d’électrons, il faudra tenir compte du fait que la mesure photométrique ne s’effectuera plus que sur 1 pixel sur quatre (le rouge) et le bilan électronique devra ainsi être multiplié par 4 pour restituer le nombre total d’électrons générés par les photons émis par Véga.
L’image V3.pic ainsi créée concerne les pixels rouges dont il faut maintenant établir la transmission spectrale. Sur base de document de chez Canon (voir Wang) , il apparaît que la courbe de transmission du filtre rouge de la matrice de Bayer (en médaillon sur la figure suivante) est de type filtre passe-haut à partir de 600nm qui englobe largement la réponse du filtre Baader-UHC .

C’est donc la fenêtre autour du pic Ha dans le rouge de ce filtre UHC qui définit la fenêtre spectrale, à savoir une largeur de 500A pour une longueur d’onde d’environ 6565A. Le calcul du nombre de photons entrant s’établit sur base de la réponse spectrale de Véga autour du pic Ha :
Débit photonique (en puissance) = 2.10-8 W/m2/µm = 2.10-16 J/s/cm2/A
Pour convertir ce résultat en nombre de photons, il est nécessaire de calculer l’énergie E d’un photon de longueur d’onde lamda=6565A
E = h.c / lamda
où h=6.62.10-34 est la constante de Planck et c=3.10+8 m/s est la vitesse de la lumière. L’énergie des photons étant d’environ 3 .10-19 J, le débit s’écrit :
Débit photonique = 666 photons/s/cm2/A
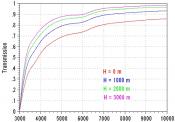
Pour une fenêtre de 500A et un temps de pose de 1s, le nombre de photons capturés par la surface collectrice de la lunette (=88 cm2) est finalement de 30.10+6 photons. Il faut cependant réduire ce résultat pour tenir compte de l’absorption atmosphérique et de la transmission optique de la lunette qui comporte 4 lentilles, soit encore 8 interfaces verre/air. Si la perte par interface est de l’ordre de 1 pourcent (revêtement multicouches de qualité), la perte pour l’optique est d’environ 8 pourcents, soit 92% de transmission. En ce qui concerne les pertes dans l’atmosphère, le graphe suivant permet d’évaluer la transmission à environ 75% à 6500A (Véga était proche du zénith et l’altitude du lieu d’observation proche de 0m). In fine, le nombre de photons collectés est donc de 21.10+6 photons.
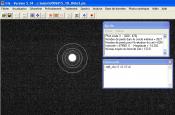
En photométrie d’ouverture (menu Analyse dans IRIS), l’intensité photométrique intégrée sur l’ensemble de l’image de Véga défocalisée s’élève à 480000 ADU. A partir du gain mesuré sur le Canon 300D (sa mesure sera l’objet d’une prochaine note), soit 2.4 électrons/ADU, la quantité totale d’électrons générés par Véga est donc de 4 X (480000 X 2.4) = 4.6.10+6 électrons.
Le rendement quantique (QE – Quantum Efficiency) du capteur CMOS de l’APN Canon 300D défiltré est finalement :
QE = 4.600.000 / 21.000.000 = 22%
Pour ceux que cela intéresse, j’ai synthétisé ce calcul sur une feuille Excel qui reprend tous les éléments nécessaires à l’évaluation du rendement quantique (voir figure ci-dessous). N’importe quelle étoile peut être utilisée pour cette mesure, pour autant que sa magnitude visuelle m, sa température effective Te et son indice bolométrique BC (ou encore son indice B-V ) soient connus. Je peux l’envoyer sur demande postée à mon adresse email : schmitz_a@swing.be

Ce résultat est en accord avec d’autres résultats de la littérature (voir Clark), et se situe bien en-dessous des performances atteintes par les CCD classiques. Différentes explications plausibles sont à avancer, dont notamment le facteur de remplissage beaucoup moins élevé lié à la technologie APS (Active Pixel Sensor, dans laquelle des composants actifs limitent la zone de conversion photoéléctrique des pixels).
D’un point de vue pratique pour l’amateur, il faudra donc s’attendre à exposer quatre fois plus longtemps avec ce genre d’appareil pour atteindre un rapport S/B équivalent à une CCD SBIG ST10, mais aussi à un prix 10 fois moindre ! Mais comme l’astrophotographie est une école de patience, le passionné mettra le temps nécessaire pour obtenir, somme toute, de très bonnes images comme il en pleut déjà au travers des revues et des sites web.
Alain SCHMITZ
14:07:40 -
schmitz a -
Catégorie : AstroBricolage
-----------------------------------------------------------------
-----------------------------------------------------------------
![]()
Total des votes : 60 - Evaluation : 3.20

